गुरुत्वमध्य (Center Of Gravity)

वस्तुमान असलेल्या प्रत्येक कणावर गुरुत्व-बल (Gravity force) कार्य करीत असते. त्या बलाला कणाचे वजन (Weight) असे म्हणतात. त्या बलाची दिशा नेहमीच अधोमुख असते. कणांच्या समूहातील प्रत्येक कणाची गुरुत्व-बल अधोमुखच असल्याने या सर्व बल परस्परांस समांतर असतात. या परस्परांस समांतर असलेल्या सर्व बलांची एक परिणामी बल काढता येते. ते परिणामी बल ज्या बिंदूतून जाते त्या बिंदूला त्या कणसमूहाचा गुरुत्वमध्य म्हणतात.

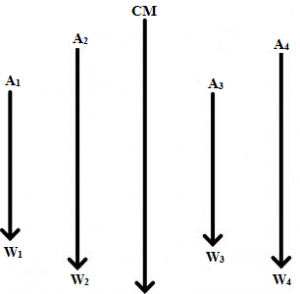
स्थैतिकीच्या (पदार्थाच्या समतोल अवस्थेचा अभ्यास करणाऱ्या शास्त्राच्या) नियमानुसार या कणांची वजने अनुक्रमे , , , आणि त्यांची सहनिर्देशक अक्षांवरील (अवकाशातील बिंदूंची स्थाननिश्चिती करण्यासाठी एका बिंदूतून परस्परांस काटकोन करणाऱ्या , , अशा तीन संदर्भरेषांवरील म्हणजे अक्षांवरील) अंतरे , , , ; , , , आणि , , , अशी असल्यास गुरुत्वमध्याचे  अक्षावरील अंतर ने दर्शवता येते. ज्याचे सूत्र खालीलप्रमाणे मांडले जाते.

अशाच रूपात आणि या अक्षांवरील अंतरे , , , इत्यादींऐवजी , , , इत्यादी व नंतर , , , इत्यादी घालून मिळतात.

वरील निरनिराळ्या समूहांऐवजी कोणत्याही वस्तूचा गुरुत्वमध्य काढण्यासाठी ती वस्तू कणांच्या समुच्चयापासून बनलेली आहे असे समजून वरील नियमाचा उपयोग करता येतो.

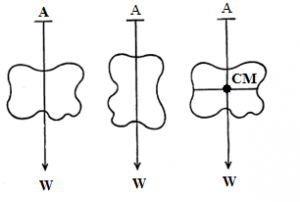
गुरुत्वमध्य एका साध्या प्रयोगानेही काढता येतो. त्यासाठी जिचा गुरुत्वमध्य काढावयाचा आहे ती वस्तू एका दोरीने टांगतात आणि त्या दोरीची दिशा दाखविणारी रेषा त्या वस्तूवर (उदा., धातूच्या पातळ पत्र्यावर) काढतात. दोरीचा ताण त्या वस्तूच्या वजनाला तोलून धरतो तेव्हा त्या वस्तूचे वजन आणि ती दोरी एकाच सरळ रेषेत असल्यामुळे दिशा दाखविणारी रेषा गुरुत्वमध्यातून जाते. नंतर ती दोरी वस्तूला निराळ्या जागी बांधून पुन्हा हीच क्रिया करतात. या दोन क्रियांतून मिळालेल्या रेषांचा छेदबिंदू हा त्या वस्तूचा गुरुत्वमध्य असतो.

ज्या वस्तूत वस्तुमान सारख्या प्रमाणात विखुरलेले असते तिचा गुरुत्वमध्य सममितीच्या (पदार्थाच्या निरनिराळ्या भागांचे आकार व रचना यांत असलेल्या सारखेपणाच्या) तत्त्वानेही काढता येतो. उदा., एकविध (सर्वत्र सारख्या असलेल्या) गोल चकतीचा गुरुत्वमध्य तिचा मध्यबिंदू असतो.

गुरुत्वमध्याप्रमाणेच वस्तुमानमध्याची व्याख्या करतात. एखाद्या वस्तूचे संपूर्ण वस्तुमान त्या वस्तूतील एका बिंदूतच एकत्रित झाले आहे असे मानता येते. अशा बिंदूला वस्तुमानमध्य म्हणतात. शुद्ध गतिविज्ञानात वस्तुमानमध्याच्या कल्पनेचा उपयोग करतात. एकविध गुरुत्वाकर्षण क्षेत्रात वरील दोन बिंदू एकस्थित (एका ठिकाणी) असतात.

व्यवहारात गुरुत्वमध्याचा फार उपयोग होतो. उदा., वाहनातील  सामानाची रचना सर्व बाजूंना सारख्या प्रमाणात केल्यास सर्व सामानाचा गुरुत्वमध्य वाहनाच्या चाकांमध्येच राहतो. त्यामुळे ते  कोलमडत नाही.

समीक्षक-संपादक – माधव राजवाडे