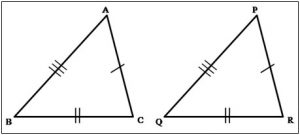
१) बाबाबा कसोटी : एका त्रिकोणाच्या (शिरोबिंदूच्या एकास एक संगतीनुसार) तीन बाजू दुसऱ्या त्रिकोणाच्या तीन बाजूंशी एकरूप असतील तर ते दोन त्रिकोण ‘बाबाबा’ कसोटीनुसार एकरूप असतात. बाजू AB ≅ बाजू PQ, बाजू BC ≅ बाजू QR बाजू AC ≅ PR म्हणून ΔABC ≅ ΔPQR.
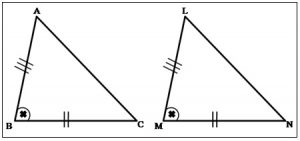
२) बाकोबा कसोटी : एका त्रिकोणाच्या दोन बाजू आणि त्या दोन बाजूंमधील समाविष्ट कोन हे घटक जर दुसऱ्या त्रिकोणाच्या दोन बाजू आणि त्यांच्यातील समाविष्ट कोन या घटकांशी एकरूप असतील तर ते दोन त्रिकोण ‘बाकोबा’ कसोटीनुसार एकरूप असतात. बाजू AB ≅ बाजू LM, बाजू BC ≅ बाजू MN आणि ∠ABC ≅ ∠LMN, म्हणून ΔABC ≅ ΔLMN
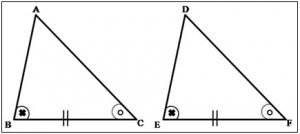
३) कोबाको कसोटी : एका त्रिकोणाची एक बाजू आणि त्या बाजच्या लगतचे दोन कोन हे दुसऱ्या त्रिकोणाची एक बाजू आणि तिच्या लगतचे दोन कोन यांच्याशी एकरूप असतील तर ते दोन त्रिकोण ‘कोबाको’ कसोटीनुसार एकरूप असतात. ∠B ≅ ∠E, ∠C ≅ ∠F आणि बाजू BC ≅ बाजू EF तर ΔABC ≅ ΔDEF.
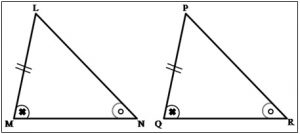
४) बाकोको कसोटी : एका त्रिकोणाची एक बाजू, तिच्या लगतचा एक कोन आणि त्याबाजूचा संमुख कोन हे तीन घटक दुसऱ्या त्रिकोणाची एक बाजू, त्या बाजू लगतचा एक कोन आणि त्या बाजूचा संमुख कोन यांच्याशी एकरूप असतील तर ते दोन त्रिकोण ‘बाकोको’ कसोटीनुसार एकरूप असतात. बाजू LM ≅ बाजू PQ, ∠M ≅ ∠Q व ∠N ≅ ∠R, म्हणून ΔLMN ≅ ΔPQR
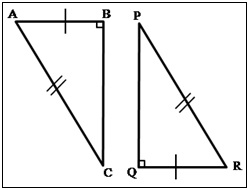
५) कर्णभुजा प्रमेय : एका काटकोन त्रिकोणाचा कर्ण आणि एक बाजू ही दुसऱ्या काटकोन त्रिकोणाचा कर्ण आणि एक बाजू यांच्याशी एकरूप असतील तर ते काटकोन त्रिकोण एकरूप असतात. काटकोन ΔABC आणि काटकोन ΔPQR मध्ये कर्ण AC ≅ कर्ण PR आणि बाजू AB ≅ बाजू RQ म्हणून ΔABC ≅ ΔRQP (या गुणधर्माला कर्ण-भुजा प्रमेय असे म्हणतात.)
समीक्षक : शशिकांत कात्रे