त्रिकोणाचे क्षेत्रफळ (Area of ​​Triangle)

आकृती क्र.१

त्रिकोणाचे क्षेत्रफळ म्हणजे त्रिकोणाच्या आंतरभागाचे (प्रतलखंडाचे; त्रिकोणी क्षेत्राने व्यापलेल्या प्रतलाच्या तुकड्याचे) क्षेत्र मापन होय. (प्रतल म्हणजे सपाट पृष्ठभाग आणि प्रतल खंड म्हणजे सपाट पृष्ठभागाचा मर्यादित तुकडा)

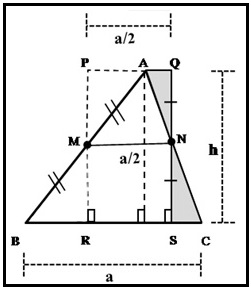
आकृती १ मध्ये बिंदू M आणि बिंदू N हे अनुक्रमे बाजू AB आणि बाजू AC चे मध्यबिंदू (बिंदू M मधून जाणारा रेषाखंड PR हा बाजू BC ला लंब आहे आणि बिंदू N मधून जाणारा रेख QS हा बाजू BC ला लंब आहे.) ΔBRM चे बिंदू M भोवती फिरवून ΔMAP दर्शविला आहे. तसेच ΔCSN‍ हा बिंदू N भोवती फिरवून ΔNAQ दर्शविला आहे.

⧠ PQRS हा एक आयत आहे. रेषाखंड MN, रेषाखंड RS आणि रेषाखंड PQ हे समान लांबीचे असून त्यांची लांबी रेषाखंड RS आणि रेषाखंड PQ हे समान लांबीचे असून त्यांची लांबी रेख BC च्या (पायाच्या) निम्मी आहे.

ΔABC ची उंची (h) ही रेख PR आहे रेख QS यांच्या लांबी एवढी आहे. ⧠ PQRS चे क्षेत्रफळ आणि Δ ABC चे क्षेत्रफळ समान आहे.

ΔABC चे क्षेत्रफळ = ⧠ PQRS चे क्षेत्रफळ

= लांबी PR × रुंदी RS

=\frac{1}{2} (पाया BC × ΔABC ची उंची)

आकृती क्र. २

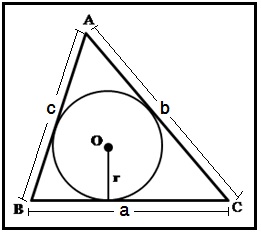
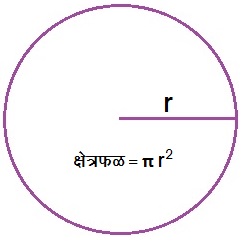
आकृती २ मध्ये बिंदू O हा ΔABC च्या आंतरवर्तुळाचा केंद्रबिंदू आहे. (त्रिकोणाच्या आंतरभागातील जे वर्तुळ त्रिकोणाच्या तिन्ही बाजूंना आतून स्पर्श करते त्या वर्तुळाला त्रिकोणाचे आंतरवर्तुळ असे म्हणतात. त्रिकोणाची प्रत्येक बाजू ही स्पर्श बिंदूत काढलेल्या त्रिज्येला लंब असते.) ΔABC चे क्षेत्रफळ हे ΔOBC, ΔOCA व ΔOAB या त्रिकोणांच्या क्षेत्रफळांच्या बेरजे एवढे आहे. r = वर्तुळाची त्रिज्या

A (\triangle ABC) = A (\triangle OBC)+ A (\triangle OCA) + A(\triangle OAB)

= \frac{1}{2} a.r + \frac{1}{2} b.r + \frac{1}{2} c.r

= \frac{1}{2} r (a+b+c)

= \frac{1}{2} r [l(BC) + l(BC)+ l(AB)]

∴ ΔABC चे क्षेत्रफळ = \frac{1}{2}आंतरवर्तुळाची त्रिज्या × ΔABC ची  परिमिती.

आकृती क्र. ३

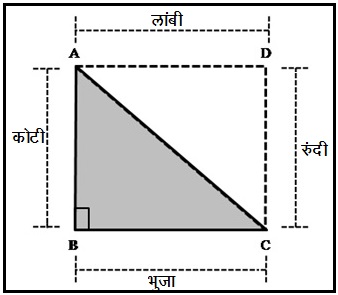
आकृती ३ मध्ये ΔABC हा काटकोन त्रिकोण आहे. ⧠ABCD  हा एक आयत आहे.

कोटी AB = रुंदी CD

भुजा BC = लांबी AD

ΔABC चे क्षेत्रफळ आयत ⧠ABCD च्या निम्मे आहे.

A (Δ ABC) = \frac{1}{2} A(⧠ABCF) = \frac{1}{2} [लांबी AD X रुंदी DC]

∴ काटकोन त्रिकोणाचे क्षेत्रफळ = \frac{1}{2} कोटी × भुजा

काटकोन त्रिकोणाचे क्षेत्रफळ काटकोन करणाऱ्या बाजूंच्या गुणाकाराच्या निम्मे असते.

आकृती क्र. ४

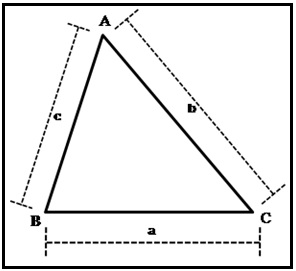
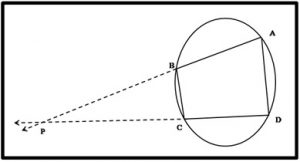
हीरोचे सूत्र :- प्रचलित संकेतानुसार ΔABC मध्ये (आकृती ४),

बाजू (BC)= l(BC) = a;

बाजू (AC) = l(AC) = b आणि

बाजू (AB)= l(AB) = c

त्रिकोणाची परिमिती = a +b + c

त्रिकोणाची अर्धपरिमिती = S = \frac{1}{2} (a + b + c)

त्रिकोणाचे क्षेत्रफळ = \sqrt{S(S-a)(S-b)(S-c)}

हीरो हा गणितज्ञ अलेक्झांड्रिया येथे इ.स. पहिल्या शतकात होऊन गेला.

आकृती क्र. ५

समभुज त्रिकोणाचे क्षेत्रफळ =  \sqrt{\frac {3}{4}} × (त्रिकोणाच्या बाजूंची लांबी)2.

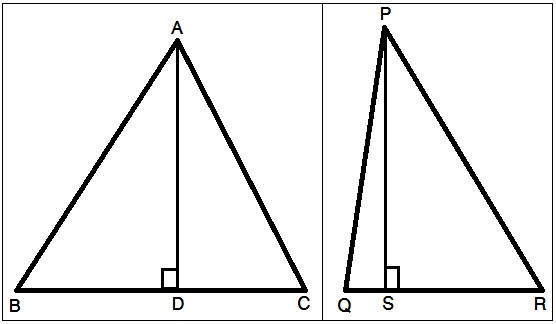
त्रिकोणाचे क्षेत्रफळांचे प्रमाण : दोन त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर हे त्यांचा पाया आणि त्या पाया संगत उंची यांच्या गुणाकाराच्या प्रमाणात असते (आकृती ५).

रेख AD ही ΔABC ची उंची; रेख PS ही ΔPQR ची उंची

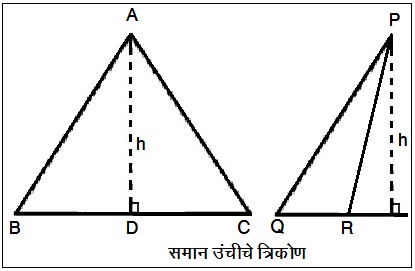
\frac {A (\triangle ABC)}{A (\triangle PQR)} = \frac{[l(BC) \times l(AD)]}{[l(QR) \times l(PS)]}

आकृती क्र. ६

समान उंचीच्या त्रिकोणांची क्षेत्रफळे त्यांच्या संगत पायांच्या प्रमाणात असतात (आकृती ६). ΔABC मध्ये रेख AD ही पाया BC संगत उंची आणि ΔPQR मध्ये रेख PS ही पाया QR संगत उंची. जर रेख AD आणि रेख PS यांची लांबी (h) समान असेल तर,

\frac {A (\triangle ABC)}{A (\triangle PQR)} = \frac{l(BC)}{l(QR)}

ΔABC आणि ΔPQR हे समान उंचीचे त्रिकोण आहेत.

पाया BC = b1 आणि पाया QR=b2

आकृती क्र. ७

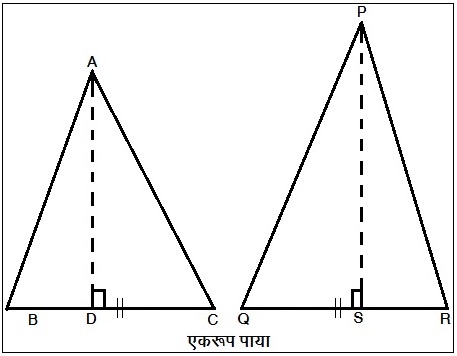
समान लांबीचा (एकरूप) पाया असणाऱ्या त्रिकोणांची क्षेत्रफळे त्यांच्या संगत उंचीच्या प्रमाणात असतात (आकृती ७). रेख AD (h1) ही पाया BC संगत उंची आणि रेख PS (h2) ही पाया QR यांची लांबी समान (एकरूप) असेल तर

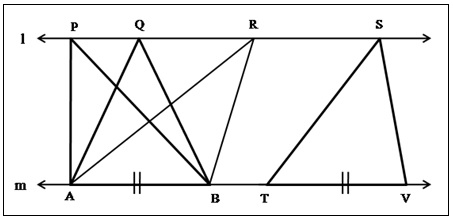
\frac {A (\triangle ABC)}{A (\triangle PQR)} = \frac{l(AD)}{l(PS)} = \frac{h_1}{h_2}

आकृती क्र. ८

एकाच (किंवा एकरूप) पायावार असणाऱ्या आणि समांतर रेषांच्या एकाच जोडीत असणाऱ्या सर्व त्रिकोणांची क्षेत्रफळे समान असतात (आकृती ८). (म्हणजे ते समक्षेत्र असतात.) ΔPAB, ΔQAB, ΔRAB आणि ΔSTV समक्षेत्र  त्रिकोण आहेत.

 

 

समीक्षक : शशिकांत कात्रे

Tags: , , , ,